트리의 개념
리스트, 스택, 큐는 선형 자료 구조이다. 선형 자료 구조란 자료들이 선형으로 나열되어 있는 구조를 의미한다. 계층적인 구조를 나타낼 땐, 트리를 이용한다.
트리의 용어
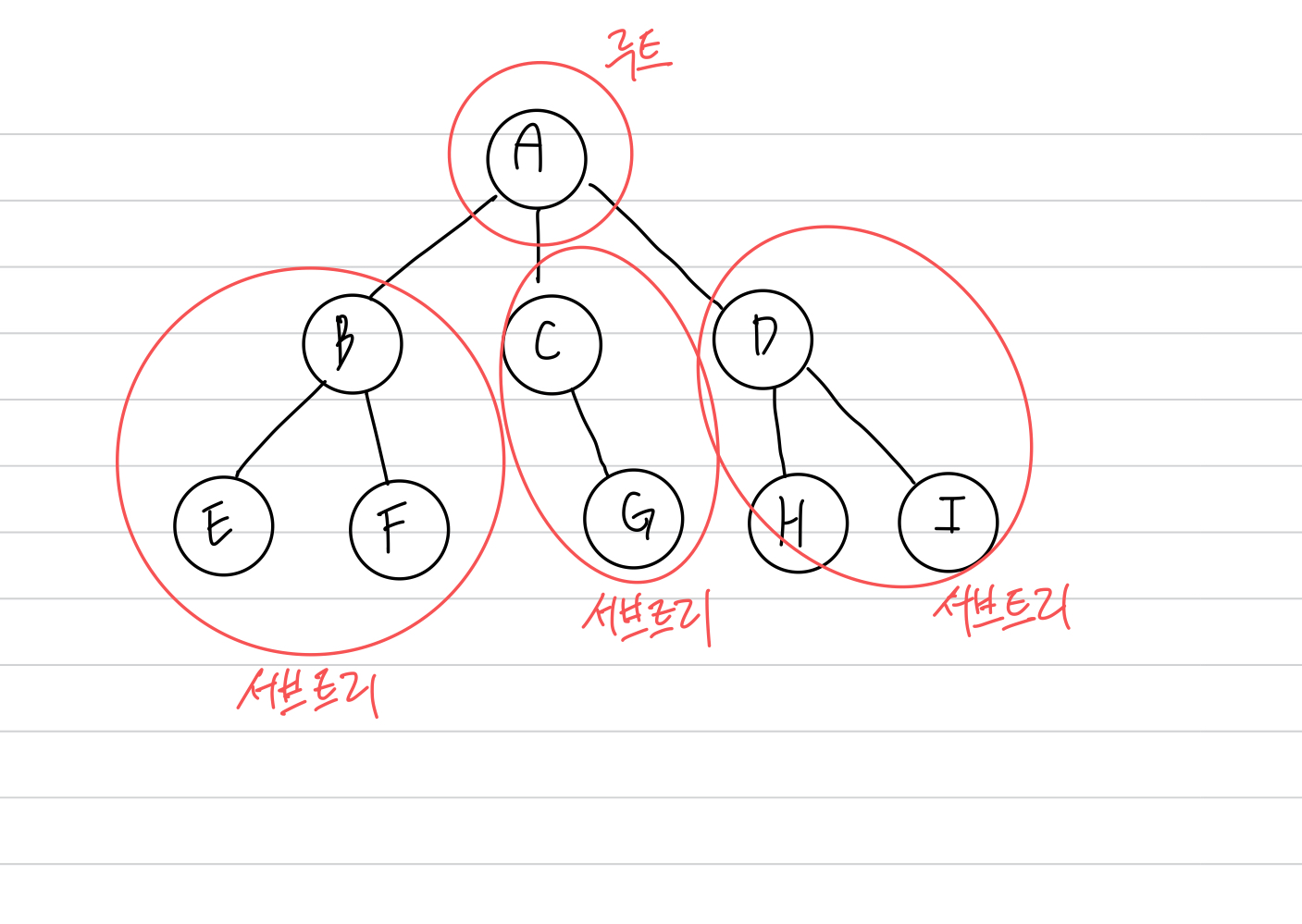
A, B, C, D .. 이런것들을 노드라고 한다. 계층의 가장 위에있는 노드를 루트노드, (B, E, F) (C, G) (D H I)를 서브트리라고 부른다. 그리고, (B E F)의 루트는 B가 되고, 나머지 E F는 서브트리가 된다. 트리에서 루트와 서브트리를 연결하는 선을 간선(edge)라고 부른다.
노드의 차수는 노드가 갖고있는 자식노드의 개수를 의미한다. A는 자식을 B C D 총 3명 가지고있으므로 차수(degree)가 3이다. B는 2개. 트리의 차수는 트리가 가지고 있는 노드의 차수중 가장 큰 값이다. 이 트리는 3차수 트리이다.
트리의 level은 트리의 각 층에 번호를 매기는 것으로, A레벨은 1, (B C D)의 레벨은 2 이렇게 흘러간다. 트리의 높이는 트리가 가지고 있는 최대 높이다. 위의 트리의 높이는 3이다.
트리의 종류
- 일반 트리 - 각 노드들이 서로 다른 개수의 자식을 가진다. -> 노드의 크기가 고정되어있지 않다.
- 이진 트리 - 자식노드의 개수가 2개
이진 트리의 정의
모든 노드가 2개의 서브 트리를 가지고 있는 트리는 이진 트리라고 한다. 서브트리는 공집합일 수 있다. 이진트리에는 최대 2개의 자식노드가 존재할 수 있다. 공집합도 이진트리이다. 또한 이진트리에는 서브트리간에 순서가 존재한다. 따라서, 왼쪽 서브트리, 오른쪽 서브트리는 서로 구별된다.

이진 트리의 종류
- 포화 이진트리 - 각 레벨에 노드가 꽉 차있는 이진트리
- 완전 이진트리 - 마지막 레벨을 제외한 모든 노드가 꽉 차있고, 마지막 레벨엔 왼쪽부터 채워져야함(빈 곳 있으면 안됨)
- 기타 이진트리 - 나머지

이진 트리의 표현
- 배열 표현
- 포인터 표현
배열 표현
포화 이진트리나 완전 이진트리의 경우 많이 쓰이는 방법이다. 트리의 깊이가 k라고 하면 최대 노드의 개수는 2^k - 1이므로, 2^k - 1개의 공간을 연속적으로 할당한 다음, 번호대로 노드들을 저장한다.

인덱스만 안다면 노드의 부모나 자식을 쉽게 알 수 있다.
링크 표현
링크 표현법에서는 노드를 구조체로 정의한다. 각 노드가 포인터를 가지고 있어서, 노드와 노드를 연결하는 방식이다. 하나의 노드가 3개의 필드를 가지는데, 데이터 저장필드, 왼쪽 자식 노드필드, 오른쪽 자식노드필드이다.

이진트리를 링크 표현법으로 그려보면 다음과 같다.

간단한 구현
typedef struct TreeNode{
int data;
struct TreeNode *left;
struct TreeNode *right;
} TreeNode; 구조체로 노드의 구조를 정의한다. 링크는 포인터의 개념을 이용한다.
TreeNode *node1;
TreeNode *node2;
TreeNode *node3;
node1 = (TreeNode *)malloc(sizeof(TreeNode));
node2 = (TreeNode *)malloc(sizeof(TreeNode));
node3 = (TreeNode *)malloc(sizeof(TreeNode));
node1->data = 10;
node1->left = node2;
node1->right = node3;
node2->data = 20;
node2->left = NULL;
node2->right = NULL;
node3->data = 30;
node3->left = NULL;
node3->right = NULL;
free(node1);
free(node2);
free(node3);
위 코드는 위 그림을 코드로 구현한 사례이다.
'자료구조(Data Structure)' 카테고리의 다른 글
| 구현해볼 자료구조와 (알고리즘) (1) | 2025.02.26 |
|---|---|
| 이진 트리의 순회 (0) | 2023.04.26 |
| 배열의 응용 : 희소 행렬 / 전치행렬 (4) | 2023.03.23 |
| C언어로 원형 연결 리스트 구현하긩 (0) | 2023.02.05 |
| C언어로 연결리스트(Linked List) 구현하기 (0) | 2023.02.03 |