순환
순환이란 어떤 알고리듬이나 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 방법이다.
순환적인 문제를 해결하는데 적합하고, '반복'을 사용하는 것 보다 간결하고 이해가 쉬울 때도 있다.
하지만, 함수를 호출하고 기억장소를 할당해야 하기때문에 반복에 비해서 비효율적이고 속도가 느릴 수 있다.
순환의 예
순환은 순환적인 문제를 해결하는데 적합하다고 했다.
예를 들어, 팩토리얼(factorial)계산은 순환적이다.
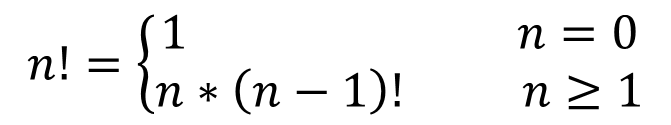
팩토리얼의 정의를 살펴보면, n!을 계산하기 위해 n에 (n-1)!을 곱한다. 즉, n!을 정의하기 위해서 다시 (n-1)!을 사용한다는 것이다.
이러한 것을 '순환적'이다 라고 한다.
이것을 재귀함수를 이용해서 풀어보자.
int factorial(int n)
{
if(n <= 1)
return 1;
else
return n * factorial(n - 1);
}factorial함수를 호출하면 n <= 1인 조건(정지조건)을 만족하기 전까지, 계속 자기 자신을 호출한다(순환).
정지조건이 없다면 무한히 함수가 반복되기 때문에, 정지조건을 넣어주어야 한다.
만약, factorial(3)을 호출한다면.
factorial(3) = 3 * factorial(3 - 1)
factorial(3 - 1) = 2 * factorial(2 - 1)
factorial(2 - 1) = 1
즉, factorial(3) = 3 * 2 * 1 이다.
계속 자기 자신을 호출하면서 factorial(3)을 완성해나가는 것을 볼 수 있다.
순환의 원리
순환은 문제의 일부를 해결하고, 나머지 문제에 대하여 순환호출을 한다.
return n * factorial(n-1)
//n은 해결한 부분, factorial(n-1)은 해결할 나머지 부분주어진 문제를 더 작은 동일한 문제로 분해해서 해결한다.
이런 방법을 '분할정복'방식 이라고 한다.
즉, 문제의 크기가 점차 작아진다.
거듭제곱값 계산
팩토리얼을 계산할 때는 '반복'을 이용하는것이 '순환'을 이용하는 것보다 더 빠르고 효율적이다.
하지만, 거듭제곱을 계산할 때는 '순환'이 '반복'을 사용할 때 보다 더 빠르다.
순환을 사용하면서 계산해야 할 양이 점점 줄어들기 때문이다.
반복
거듭제곱 계산을 반복을 이용해서 만들어보자.
double power(double x, int n)
{
double result = 1;
for(int i = 0; i < n; i++){
result = result * x;
}
return result;
}x를 n번 곱하는, 즉 x^n을 구하는 함수이다.
순환
이번에는 순환을 이용해서 함수를 만들어보자.
순환을 이용해서 거듭제곱을 구하는 함수는 2가지 방법으로 만들수 있다.
1 방법)
double power(double x, int n) {
if(n == 0)
return x;
else
return x * power(x, n - 1);
}가장 쉽게 생각할 수 있는 방법
2 방법)
(1) n이 짝수일 때

이렇게 계산하고.
(2) n이 홀수일 때

이렇게 계산한다.
위 2가지 조건을 이용해서 순환 함수를 작성해보면,
double power(double x, int n)
{
if(n == 0)
return 1;
else if(n % 2 == 0) //짝수
return power(x * x, n / 2);
else //홀수
return x * power(x * x, n - 1 / 2);
}만약, 이 논리가 이해가 안되면,
직접 손으로 2의5승을 이 직접 이 함수를 이용해서 공책에 써보도록 하자.
그렇다면 왜 이 경우에는 순환을 사용하는게 더 빠를까?
함수를 호출할 때 마다 문제의 크기가 절반씩 줄어들기 때문이다!
만약 n = 100이라면, 다음함수를 호출하면 n = 50, 또 호출하면 n = 25 계속 절반씩 감소한다.
피보나치 수열의 계산
피보나치 수열을 순환을 사용해서 구현할 수 있다.
가독성이 좋고, 간단하게 작성할 수 있다.
하지만, 비효율성을 가져올 수 있으니 주의하자.
피보나치 수열이란, 앞의 두 개의 숫자를 더해서 뒤의 숫자를 만드는 수열이다.
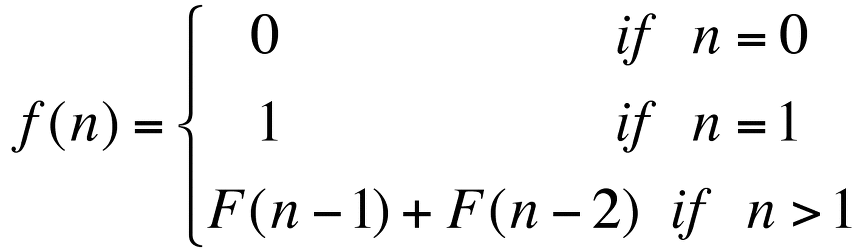
정의는 이렇다. 수열을 쭉 나열 해보면
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ....
이런식으로 나열된다.
피보나치 수열을 순환으로 구현해보자.
int fibo(int n)
{
if(n == 0)
return 0;
else if(n == 1)
return 1;
else
return fibo(n - 1) + fibo(n - 2);
}구현이 쉽고, 가독성이 좋다.
피보나치는 정의 자체가 순환적으로 되어있기 때문에, 순환을 이용하는것이 당연해 보인다.
비효율성
하지만, 순환으로 피보나치를 구현한다면 상당히 비효율적이다.
why?
만약 fibo(6)을 호출한다면, fibo(4)는 2번 fibo(3)은 3번이나 호출되기 때문이다.
즉, 같은게 여러번 호출된다.
n = 30이면 300만번의 호출이 필요한데,
n이 점점커진다면 수열을 계산하는건 불가능에 가깝다.
이 경우에는 '반복'을 사용하는것이 효율적이다.
반복으로 피보나치수열을 구현해보자.
int fibo(int n)
{
if(n == 0)
return 0;
else if(n == 1)
return 1;
int pp = 0; //전전 수
int p = 1; //전 수
int result = 0;
for(int i = 2; i <= n; i++){
result = p + pp; //전전 수 + 전 수
pp = p;
p = result;
}
return result;
}
하노이탑 문제
하노이탑 문제를 한번 쯤 들어봤을 법한 문제이다.
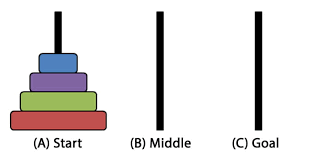
A지점에 있는 원판들을 C로 옮기면 되는데, 3가지 규칙이 존재한다.
1.한 번에 하나의 원판만 이동가능
2.맨 위의 원판만 이동가능
3.크기가 작은 원판위에 큰 원판이 쌓일 수 없다.
이 문제를 풀기에는 순환을 사용하는게 효과적이다.
순환이 일어날수록 문제의 크기가 작아지기(옮길 원판 수)때문이다.
해결방법)
1.가장 밑에 있는 원판 1개, 그리고 가장 밑에 있는 원판 1개를 제외한 나머지 원판의 개수를 n-1개 라고 하자.
2.n-1개의 원판을 B막대로 모두 옮긴다.
3.남아있던(가장 밑에 있는)원판을 C로 옮긴다.
4.B에 있는 n-1개의 원판을 모두 C로 옮긴다.
문제)
원리는 알겠지만, n-1개의 모든 원판을 어떻게 옮기지?, 하나씩 옮겨야 하는데? 라고 생각이 들 것이다.
그래서 순환을 사용한다. why? 문제의 크기가 계속 작아져 1개의 원판씩 옮기는 것과 같다.
코드)
void hanoi(int n, char from, char temp, char to)
{
if(n == 1){
printf("원판 1을 %c 에서 %c으로 옮긴다.\n", from, to);
}
else{
hanoi(n - 1, from, to, temp); //temp로 이동
printf("원판 %d를 %c 에서 %c으로 옮긴다.\n", n, from, to);
hanoi(n - 1, temp, from, to); //to로 이동
}
}ex) hanoi(3)을 입력하면, hanoi(2)가 호출되고, 이것은 또 hanoi(1)이 호출된다.
만약 이해하는게 힘들면 hanoi(2)를 직접 손으로 써보면서 이해하면 된다..
hanoi(2)를 호출했다고 가정했을 때,

이런 순서로 순환이 된다.
관련 문제
백준 10870번
백준 2737번
백준 2748번
'자료구조(Data Structure)' 카테고리의 다른 글
| C언어로 덱(Deque) 구현하기 (2) | 2023.01.31 |
|---|---|
| 원형큐 구현하기 (2) | 2023.01.25 |
| C언어로 큐(Queue) 구현하기 (0) | 2023.01.23 |
| 동적 배열 스택 구현하기 (0) | 2023.01.23 |
| C언어로 스택(Stack) 구현하기 (0) | 2023.01.21 |